Hasta ahora sólo he presentado juegos de plataformas algo… estáticos. ¿Dónde quedan esas plataformas tan estresantes o deseadas que pueden moverse por el mapa? Estuve revisando un par de tutoriales que hay sobre esta mecánica, y me gustaría compartir uno que me ha gustado y no es tan difícil de implementar.
Les hablo del tutorial de Game Endevor. También hay un video genial de GDQuest, pero involucra el modo “tool” de los scripts… cosa que no he explicado previamente y puede generar más dudas de las esperadas. En un futuro no muy lejano cubriré ese tutorial también, porque es muy interesante.
Por ahora no me enredo más. Empecemos con la adaptación de Game Endevor:
Paso 1: Crear la escena de la plataforma móvil
Recuerden que estamos en un entorno de dos dimensiones. La nueva escena tendrá como nodo principal un “Node2D” y dentro, su hijo será la plataforma que estaremos moviendo. Una plataforma que se mueve deja de ser un cuerpo estático para convertirse en un cuerpo cinemático (KinematicBody2D), quiere decir que podemos desplazarlo de una posición a otra.
Además, el Node2D tendrá como hijo un nodo de tipo “Tween” que se encargará de realizar el movimiento de la plataforma. Para los que no conocen el nodo Tween, sepan que se trata de una alternativa al nodo AnimationPlayer, que, a diferencia de este último, se maneja con código y no con una herramienta visual.
Ya deberían saber que dentro de su KinematicBody2D hace falta añadir un nodo para la colisión que desean: sea poligonal o un simple CollisionShape2D. Del mismo modo necesitan un nodo que sea la imagen de la plataforma. Miren cómo queda mi estructura de nodos:
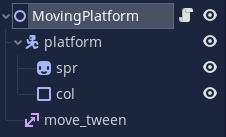
El nodo “col” es el CollisionShape2D y “spr” supongo que ya lo identifican como un Sprite. Ahora les mostraré cómo se ve dentro del juego:
Ya contamos con todos los nodos que necesitamos. Mi “plataforma” es esa concha 😂️.
Paso 2: Agregar el script a la raíz de la escena
Vamos a continuar agregando un script en el nodo “MovingPlatform” (Node2D), que es el nodo raíz. Guárdenlo donde quieran, lo primero que escribiremos ahí será esto:
extends Node2D export var idle_duration: float = 1.0
La variable “idle_duration” representa el tiempo medido en segundos, que estará detenida nuestra plataforma antes de empezar a moverse. Si quieren traumar al jugador, pueden usar un valor como de 0.5. Nota: Los dos puntos indican el tipo de dato que siempre tendrá la variable: “float” o número con decimales… la palabra reservada “export” es para editar el número desde el inspector y evitarnos modificar el script.
export var move_to: Vector2 export var cell_size: Vector2 export var speed: float = 3.0 var follow: Vector2 = Vector2.ZERO onready var platform = $platform onready var tween = $move_tween
También necesitaremos otras variables “export” que podamos modificar desde el inspector de Godot. Una de estas es el “move_to”, un Vector2. Dentro de esa variable indicaremos la cantidad de celdas que podemos desplazar esta plataforma. Digo celdas porque en la mayoría de juegos 2D estamos acostumbrados a usar TileMaps o tiles de un determinado tamaño. Cada tile ocupa una celda… entonces nosotros diremos en el inspector cuantas de estas celdas vamos a recorrer horizontal o verticalmente.
La siguiente variable es “cell_size” y como dije: es el tamaño que tienen los tiles en su juego. Generalmente son 32×32, 16×16, etc. Sus valores también los indicaremos desde el inspector de Godot.
La aceleración (speed) supongo que ya saben para qué es. Con ella definimos cuánto tarda en desplazarse la plataforma.
Cerrando con las variables “export”, hay lugar para una llamada “follow” o “seguir” en nuestro idioma. Esa variable se encargará de guardar la posición a la que se dirige la plataforma. Más abajo hablaré más sobre ella.
Las últimas dos variables no son obligatorias, pero pueden aprovecharlas. Son para guardar la dirección de los nodos que son hijos del contenedor de este script, es decir, el Node2D. Si ponen el símbolo de dólar les autocompletará el nombre de los nodos que son hijos y nietos. Nosotros sólo vamos a guardar la dirección del nodo “platform” y el nodo “move_tween”, que vieron en la estructura de nodos 👆️. Nota: cuando no estás dentro de una función y quieres guardar en una variable la dirección de un nodo hijo, tienes que poner antes de la palabra “var”, el “onready”.
Funciones dentro del Script
func _ready() -> void: init_tween()
Sólo haremos una cosa cuando se ejecute la escena de la plataforma: iniciar una función personalizada llamada “init_tween”. Así que después de esa instrucción, pasemos a crear la nueva función.
func _init_tween() -> void: move_to = move_to * cell_size
Lo primero que haremos dentro de la función será convertir las unidades que indicamos en el inspector, al tamaño que tienen las celdas de nuestro mapa. Por ejemplo: si introducimos en la variable “move_to” un valor de Vector2(10, 0), y el tamaño de las celdas es Vector2(16, 16), se multiplicará la parte horizontal de la primera variable con la parte horizontal de la segunda, y así con el eje vertical. Es decir, que move_to será igual a Vector2(10 * 16, 0 * 16).
Seguimos la función con lo siguiente:
func _init_tween() -> void: move_to = move_to * cell_size var duration = move_to.length() / speed
La duración de ese movimiento se calcula según la distancia que recorrerá entre la velocidad de la plataforma. Esta es una formula conocida en el movimiento rectilíneo uniforme: distancia = velocidad * tiempo. Para despejar el tiempo tenemos que: Tiempo = distancia / velocidad, tal como hacemos en la línea de código. Nota: para obtener la distancia del vector “move_to” tenemos que usar la función “.length()” que tienen todos los vectores, ya que de esa forma obtenemos la longitud del vector.
Seguimos dentro de la función _init_tween():
func _init_tween() -> void: move_to = move_to * cell_size var duration = move_to.length() / speed tween.interpolate_property(self, "follow", Vector2.ZERO, move_to, duration, Tween.TRANS_LINEAR, Tween.EASE_IN_OUT, idle_duration) tween.interpolate_property(self, "follow", move_to, Vector2.ZERO, duration, Tween.TRANS_LINEAR, Tween.EASE_IN_OUT, duration + idle_duration * 2) tween.start()
La siguiente línea es para tomar la variable “tween” (que es el nodo “move_tween”) y acceder a su función “interpolate_property”, que necesita varios parámetros para funcionar. Esta función lo que hace es tomar un valor inicial y uno final, para calcular el camino que debe seguir el primer valor para llegar al final. Por ejemplo: interpolar la posición inicial hasta unos doscientos pixeles, haría que podamos ver la posición en cada segundo (según la duración del Tween), en la pantalla. Esto es justo lo que vamos a hacer, con un ligero cambio.
El primer parámetro de la función “interpolate_property” es el nodo cuya propiedad vamos a interpolar. Somos nosotros mismos, así que usamos “self”. Como segundo parámetro nos pedirán el nombre de la propiedad que vamos a interpolar. Si dejan el mouse en una de las propiedades del inspector, van a obtener el nombre de esa propiedad:
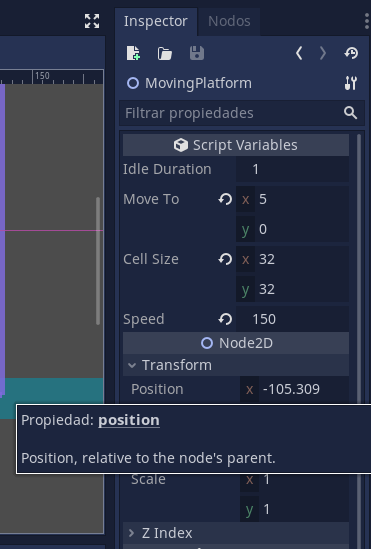
Sin embargo no necesitamos una propiedad de las que tienen siempre los Node2D. Cuando creamos una variable dentro de un nodo, automáticamente estamos tratando con una nueva propiedad. Lo que quiero decir, es que la “nueva propiedad” que vamos a interpolar, es la variable “follow” que creamos arriba.
El siguiente parámetro (ya es el tercero) es el valor inicial de esa propiedad. Recuerden que es un Vector2, empezamos con 0. Como es lógico, el segundo parámetro es para el valor final de nuestra propiedad, es decir el valor al que queremos llegar. No es otra cosa que la variable “move_to”.
Continuamos con el otro parámetro. Esta vez se trata de la duración total de nuestra “animación”. Ya tenemos una variable para eso, la que definimos arriba 👆️.
¡No se rindan! voy a traer el código para que vuelvan a ver por dónde vamos:
tween.interpolate_property(self, "follow", Vector2.ZERO, move_to, duration, Tween.TRANS_LINEAR, Tween.EASE_IN_OUT, idle_duration) tween.interpolate_property(self, "follow", move_to, Vector2.ZERO, duration, Tween.TRANS_LINEAR, Tween.EASE_IN_OUT, duration + idle_duration * 2) tween.start()
Ya indicamos cuánto tardará esa interpolación. Ahora el siguiente parámetro es para el tipo de transición, este tema me puede extender más o menos, así que en otro artículo les explicaré qué son los tipos de transición… por ahora elijan Tween.TRANS_LINEAR. El otro parámetro de “Tween.EASE_IN_OUT” se refiere al tipo de ecuación de aceleración que queremos usar. Pueden acceder a un poco más de información sobre estas ecuaciones en este vídeo 👌️.
Sólo nos falta un parámetro que sirve para indicar cuánto tiempo tarda la animación en empezar. Como justo es el primer movimiento que realiza la plataforma, decimos que tarde lo que dice la variable “idle_duration”.
¡Felicidades! Ya la plataforma puede moverse hasta el punto objetivo. Ahora tenemos que regresar al punto inicial. Volvemos a interpolar la propiedad “follow”, pero esta vez el parámetro del “valor inicial” es “move_to” (el final, donde nos encontramos ahora) y el valor final donde tiene que llegar es la posición (0, 0) o Vector2.ZERO.
También cambia el último parámetro: ahora la interpolación no puede iniciar en el mismo tiempo de detenido porque entonces se activarían las dos animaciones. ¿Cuánto tiene que esperar para iniciar entonces? La respuesta es sencilla: debe empezar después de que termine la primera animación más el tiempo que estuvo detenida (duration + idle_duration) y además sumar la duración que ella misma tendrá detenida. Es decir: duration + (idle_duration * 2).
La última línea es para iniciar el Tween. Una vez iniciado, empezará a contarse el tiempo de detenido que indicamos en el último parámetro de ambas interpolaciones y cuando terminen, se ejecutarán tal como queremos.
Faltaría sólo una función para terminar con el script:
func _physics_process(delta): platform.position = follow
La función _physics_process(delta) se ejecuta en cada frame del juego. Es una función propia de Godot. Su parámetro “delta” es el tiempo que transcurre en cada frame.
Resulta que cambiando el valor de la variable “follow” todavía no veremos un desplazamiento en nuestra plataforma. Hay que indicar que la posición del nodo “platform” (lo definimos arriba) es igual a follow. ¡Por ahora listo! pero pendientes porque volveremos aquí rápidamente.
Salgan un momento del script y hagan clic sobre el nodo “move_tween”:
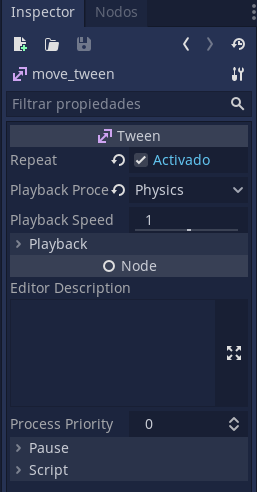
Hay que decirle que una vez iniciado, se siga repitiendo infinitamente y además que su modo de proceso sea físico, así ejecutará sus animaciones desde la función _physics_process.
Vayan al nodo raíz y cambien los valores de las variables que creamos en el script, a su antojo.


El movimiento es algo… ¿brusco? Hay una forma de hacer esto más suave cuando estás terminando el desplazamiento. Regresen al script principal de la plataforma.
En la función _physics_process cambiarán ligeramente la línea que teníamos:
func _physics_process(delta): platform.position = platform.position.linear_interpolate(follow, 0.075)
Ahora en lugar de actualizar directamente a la posición que tiene la variable “follow”, vamos a interpolar (sí, otra vez) el valor actual de la posición que tiene la plataforma (un vector) con el vector follow.
El método de interpolación entre dos vectores que podemos usar es “linear_interpolate()” y forma parte de las funciones de un vector. Su sintaxis es la siguiente: el punto A viene siendo el vector que queremos interpolar (position), hacemos un llamado a “linear_interpolate()” y como primer parámetro indicamos el punto B. Un último parámetro “amount”, es la proximidad de un punto intermedio con el punto A o el punto B.
¿Nunca antes habían interpolado dos vectores? yo tampoco… pero la teoría es bastante sencilla: tenemos un punto A y un punto B, la interpolación entre ambos nos dará un valor que no conocemos que está dentro del rango. Si A es 5 y B es 10, la interpolación puede devolver un 7.
Nosotros podemos influir en la interpolación usando el último parámetro de la función “linear_interpolate”. Como pueden ver en la documentación de Godot:

La “t” debe ser un número entre el 0.0 y 1.0. Cuando la t es 1.0, la interpolación devuelve el punto B, y cuando t es 0.0, la interpolación devuelve el punto A.
Para el efecto que estamos buscando en este tutorial, nos basta con una interpolación al 0.075, es decir, un valor bastante cercano al primer vector, que es el de la posición.
Al principio puede ser complicado esto de las interpolaciones, también hay un artículo de la documentación oficial de Godot sobre el tema, se los dejo aquí 👈️.
Reproduzcan la escena otra vez. ¿Pueden notar la diferencia?

Paso 3: Hacer que el jugador pueda subir y mantenerse…
Por fortuna esto no es tan complicado si están usando un cuerpo Kinematic2D para el personaje. Diríjanse a la función donde usan “move_and_slide()”.

El cambio radica en que no usaremos “move_and_slide” sino “move_and_slide_with_snap“. Esta nueva función nos permite añadir un tercer parámetro para la cantidad de “snap” que tiene el cuerpo mientras se mueve.
Nota: Godot añadió esta característica en la versión 3.1, así que los usuarios de 3.0 u otra versión anterior, llegan hasta aquí.
Este snap sirve para ajustar aún más el cuerpo con el suelo. Sin embargo, tengan en cuenta que si saltamos y tenemos el snap en 32, el cuerpo detectará el suelo antes de estar encima de él. Quedando unos pixeles en el aire.
Cuando la velocidad vertical no sea igual a 0 (porque está efectuándose un salto o estamos cayendo) el snap volverá a ser 0 para que podamos tocar el piso tranquilamente.
El último parámetro es un valor booleano “stop_on_slope” para que indiquemos si vamos a detener el cuerpo o no, cuando nos encontremos en una pendiente. Ponemos que sea “false” y estamos listos.
Sólo falta un detalle: diríjanse al nodo de la plataforma y activen su sincronización con la física. De esta forma, cuando el personaje esté sobre esa plataforma, no actualizará su posición unos microsegundos después que ella.

¡Terminamos! Si tienes una duda o recomendación, déjala por acá.





podrias hacer un video tutorial de barras moviles pero touch para smarthphones? usando el move_and_collide para detectar los bordes de la pantalla. gracias.