Mecánica de Movimiento en Juegos de Carreras

En la lista de tutoriales me dejaron la petición de las mecánicas para un juego de carreras. No he podido desarrollar el demo completo, tuve chance de estudiar un poco sobre las formulas de movimiento que podemos aplicar para los vehículos. Este método lo aplicó GDQuest en un repositorio que data del 2017, y usaba un auto como ejemplo. Yo usaré un barco, el funcionamiento es el mismo.

El objeto que moveremos debe tener como nodo principal un KinematicBody2D. Dentro ubicaremos la imagen y su colisión, como hacemos siempre ante este tipo de nodos. Añadimos el Script principal y empezamos con lo siguiente:

1. Cuando usamos la palabra reservada “const” estamos definiendo una constante. Las constantes son aquellos tipos de dato que después de guardarse no pueden variar su valor. Cuando decimos que la masa será 5, no podremos cambiarlo más. Generalmente las constantes se escriben en mayúsculas para diferenciarlas rápido de una variable. Para este ejemplo estamos creando cuatro constantes: una para la masa, otra para la velocidad máxima que podemos alcanzar y un par para la aceleración y desaceleración.
2. Necesitamos unas variables para la velocidad y el ángulo a donde nos movamos. Las primeras guardan números con decimales (flotantes), el resto guardará vectores. El “movimiento objetivo” que es el lugar adonde nos queremos mover según nuestro movimiento actual (target_motion), el movimiento (motion) que recibe los cálculos de la aceleración y demás, la variable steering o “dirección hacia” que guardan los puntos adonde llegaremos aplicando una determinada velocidad y por último la variable de dirección que se encarga de las entradas de teclado.

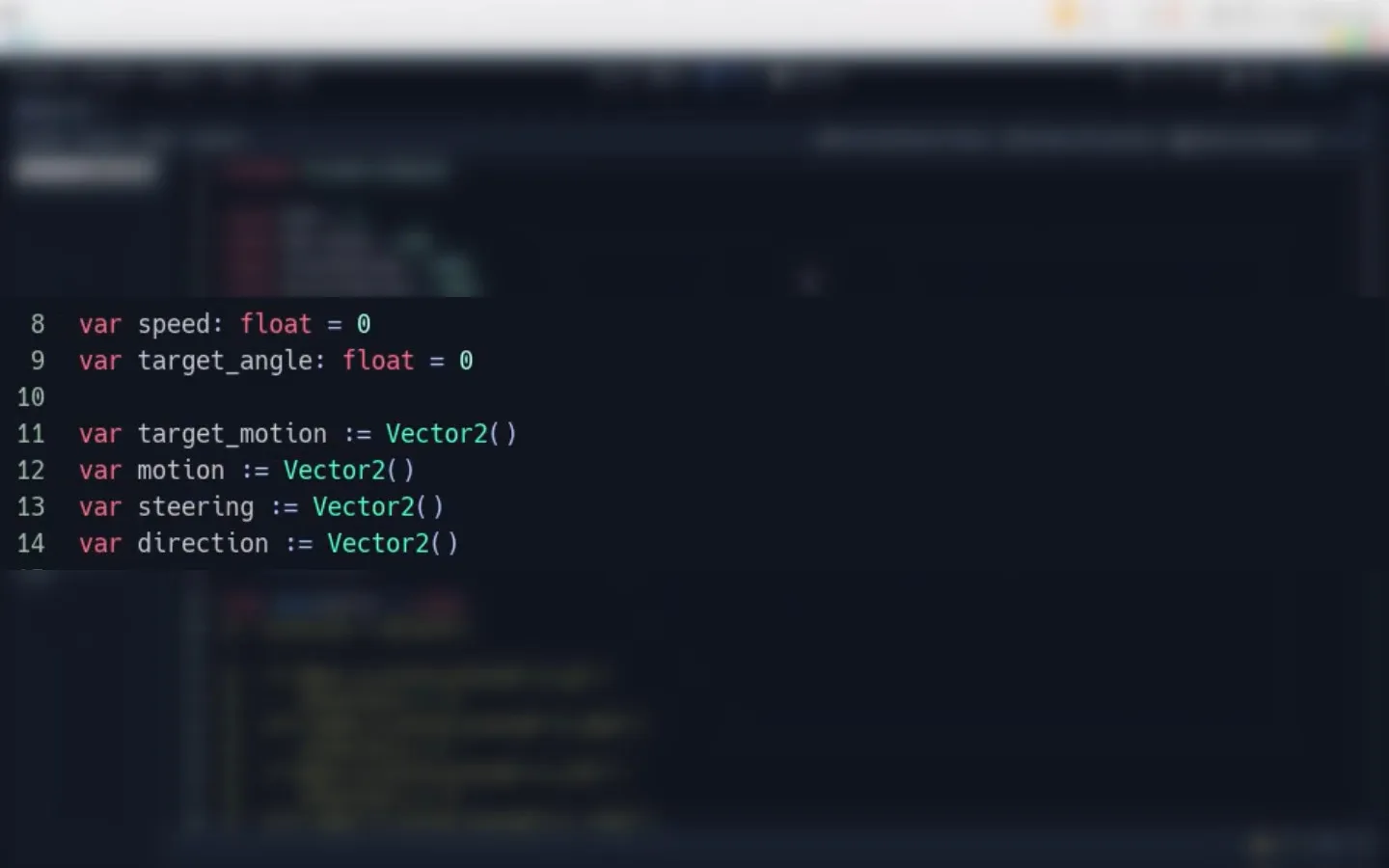
Ya con nuestras constantes y variables definidas, podemos pasar a darles uso. En la función de física llamen a una función personalizada llamada “move” y le pasan el parámetro delta para que podamos usar dentro de ella el tiempo.

Lo primero que haremos dentro de la función move(delta) será darle un valor 1 o -1 a la propiedad X y Y de la variable dirección. Si no entienden el truco que estoy aplicando, pueden eliminar esas dos líneas y escribir la parte que está comentada en esta imagen. Después de tener la dirección añadimos la comprobación de que al presionar cualquier tecla, es decir, que la dirección no sea Vector2(0,0), sumemos a la velocidad la aceleración por el tiempo, que es delta. De lo contrario, si no hay ninguna tecla presionada, restamos la desaceleración por el tiempo.

Es importante que mientras sumamos la aceleración o desaceleración, la velocidad no supere su máximo y tampoco se reduzca a menos de 0. Para eso decimos que la velocidad se regule entre el 0 y el máximo, con el método clamp(). Cuando la velocidad sea mayor que 500, automáticamente volverá a 500, y si es menor que 0, volverá a este.

Ya que tenemos la velocidad podemos darle un valor a la variable de movimiento objetivo, para que sea igual a la velocidad, por la dirección y el tiempo. Esto nos dará como resultado cada décima de segundo que alguna tecla de movimiento este presionada, que el objeto apunte a una nueva posición adonde quiera llegar. Después diremos que la variable “dirección a” o steering, sea igual al movimiento objetivo que queremos recorrer, menos el movimiento actual. En ese momento el movimiento será 0, por lo que sólo estamos guardando el punto al que queremos llegar.

Ahora comprobamos que la longitud de esa dirección sea mayor que uno para normalizarla. Si no hacemos esto los cambios en las velocidades no tendrán una transición cuando variemos la dirección. Al estar normalizando un Vector2 estamos obteniendo una longitud menor que una unidad, capaz de llevar el mismo sentido que el otro valor mayor a uno.

La primera vez que se ejecutó esta función el movimiento era cero, ahora le sumaremos la dirección a donde debe moverse y lo dividiremos en la masa. Así tendremos un efecto de lentitud según la masa del cuerpo físico. Si la velocidad vuelve a ser cero, entonces el movimiento igual. Ya sólo faltaría decirle a Godot que todo eso que hemos calculado con un razonamiento de físicos profesionales, lo ejecutará en el método de movimiento y colisión de los KinematicBody2D.

Para terminar con este tutorial vamos a añadir una comprobación para cambiar el ángulo del cuerpo según el movimiento que estamos realizando. Entonces: si el movimiento no es Vector2(0,0) digamos que el ángulo que buscamos es igual a la tangente del movimiento en su eje horizontal y vertical más la constante PI entre 2. Esto no es más que una fórmula trigonométrica.

Conociendo el ángulo que necesitamos digamos que la rotación del cuerpo (rotation) sea igual al valor negativo del mismo.

Con este tenemos un bonito barco, sacar de esto un juego de carreras ya es más completo y amerita mucho tiempo. A medida que aumente el apoyo en la plataforma de Patreon podré permitirme dedicar más tiempo al desarrollo de demos más complejos.